You always noticed that in the world where you are living things tend to move around a lot and this fascinates us to study the science of motion. Motion is the phenomenon in which a body changes its position over time. Mathematically, you can describe the motion of a body in terms of distance, displacement, speed, velocity, acceleration, and time. In a given reference frame, if an object is not changing its position with time then the object is said to be at rest or motionless.
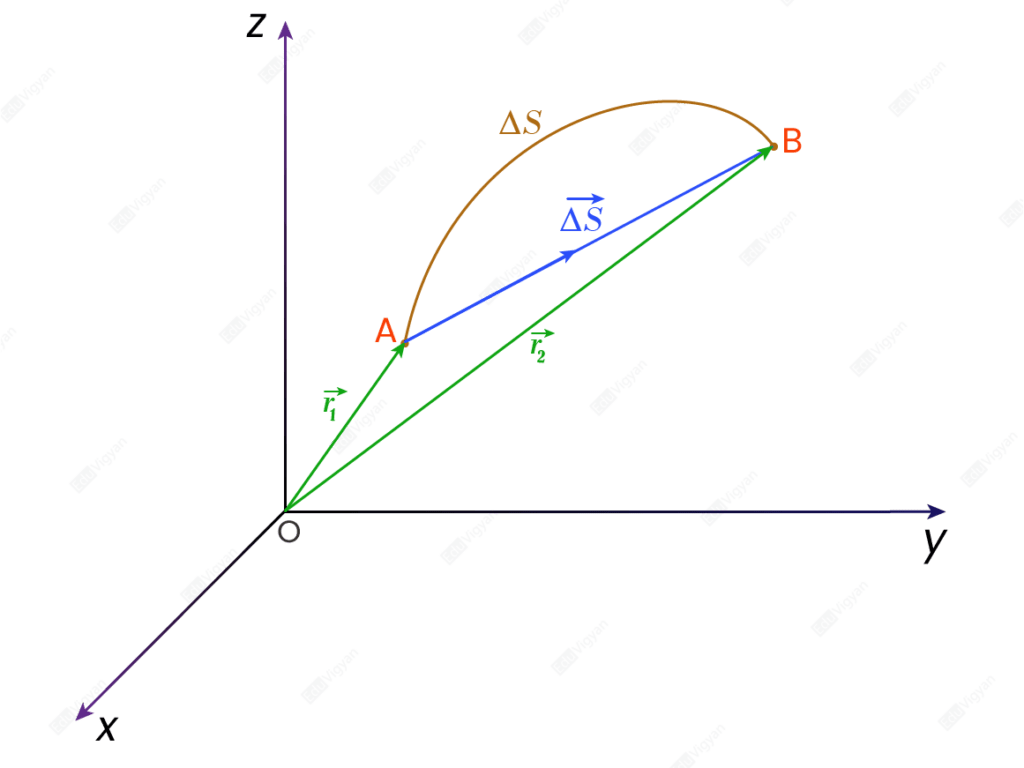
Distance (\Delta S)
The length of the actual path between the initial and final position of an object in a given time interval is called the distance travelled by the object.
Distance is a scalar quantity and its SI unit is meter. (1 meter = 100 centimetre)
Displacement (\vec{\Delta S})
The shortest distance from the initial to the final position of a moving object is called displacement.
It doesn’t depend on the path followed by the object, depends only on the initial and final position of the object.
It is the relative position of the final position of the object to the initial position. It is a vector quantity and its SI unit is meter. Mathematically, it is the difference between the position vector of the final position and the position vector of the initial position. That is,
\begin{aligned}\vec{\Delta S} &= \vec{r_2} – \vec{r_1}\\\end{aligned}
Average Speed (v)
Average speed is the total distance travelled by an object divided by elapsed time.
If an object travels a total distance of \Delta S in time \Delta t then the average speed of the object will be
\begin{aligned}v &= \dfrac{\Delta S}{\Delta t}\\\end{aligned}
Speed is a scalar quantity and its SI unit is \rm \ m/s.
Average Velocity (\vec{v})
Average velocity is the total displacement travelled by an object divided by elapsed time.
If an object travels total displacement of \vec{\Delta S} in time \Delta t then the average velocity of the object will be
\begin{aligned}\vec{v} &= \dfrac{\vec{\Delta S}}{\Delta t}\\\end{aligned}
Velocity is a vector quantity and its SI unit is \rm \ m/s.
Activity
Let’s consider Mohan is going for a long drive with his friends by a car. Right now they are at Mumbai and are going to Delhi. For this Mohan is going to open a Google map. Let’s try to obtain the distance, displacement, average speed and average velocity during their journey. In the Google map (shown below), the deep blue curve is the most suitable path suggested by the Google. If they will follow this path and drive nonstop then it will take 25\rm \ hours to reach at Delhi. And they will have to travel 1417\rm \ km in those 25\rm \ hours.
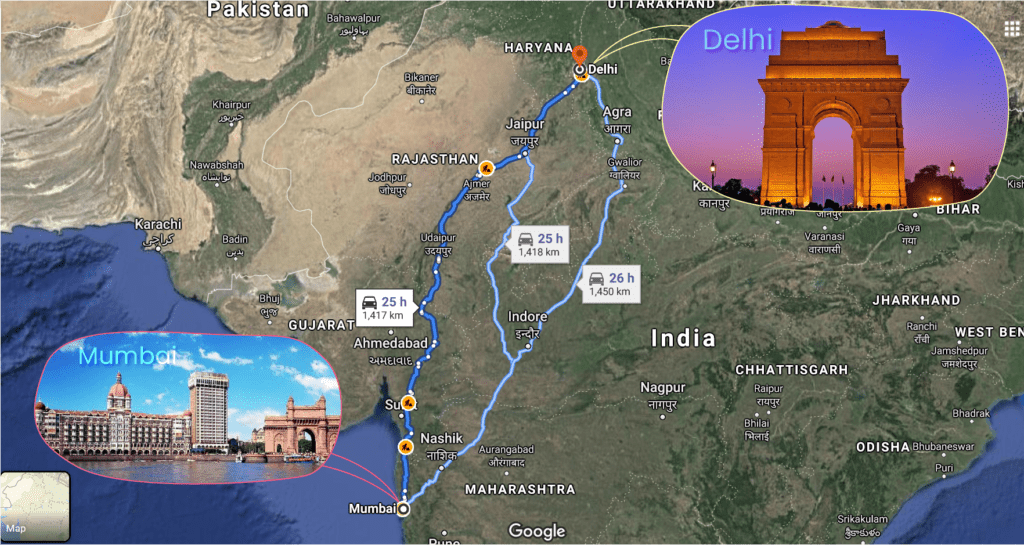
The distance travelled by car in one side trip, that is trip from Mumbai to Delhi is;
\begin{aligned}\Delta S &= 1417\rm \ km\\\end{aligned}
The time taken is;
\begin{aligned}\Delta t &= 25\rm \ h\\\end{aligned}
What will be the average speed of their car?
Since the average speed is the ratio of the total distance travelled by car in total time taken so it will be
\begin{aligned}v &=\dfrac{\Delta S}{\Delta t}\\&= \dfrac{1417\rm \ km}{25\rm \ h}\\&= 56.68\rm \ km/h\\\end{aligned}
How do you calculate the displacement?
As they know the displacement is the minimum distance between two points but this is not the complete definition of the displacement. Since displacement is a vector quantity so it must have some direction also. In the map (shown below), the East direction is along rightward and the north direction is along upward.

Since the total straight line distance between Mumbai and Delhi is around 1153\rm \ km and the angle made by this straight line with the east direction is around 69^0 so the displacement will be
\begin{aligned}\vec{\Delta S} &= 1153 \rm \ km, 69^0\ North\ of \ East\\\end{aligned}
This is the displacement when they are travelling from Mumbai to Delhi. But what would be the displacement in our return journey? That is our journey from Delhi to Mumbai.
In our return journey, the magnitude of the displacement will be the same but the direction will be the opposite. It will be
\begin{aligned}\vec{\Delta S} &= -1153 \rm \ km, 69^0\ North\ of \ East\\ &= 1153 \rm \ km, 69^0\ South\ of \ West\\\end{aligned}
If you want to figure out the total displacement during our journey then it will be
\begin{aligned}\vec{\Delta S} &= 0\\\end{aligned}
What would be the average velocity of this car?
For the one side trip from Mumbai to Delhi, average velocity will be
\begin{aligned}\vec{v_1} &= \dfrac{1453\rm \ km\ 69^0\ North\ of \ East }{25\rm \ Hrs}\\&= 46.12\rm \ km/h\ 69^0\ North\ of \ East\\\end{aligned}
Here is a question for you.
- Find the average velocity of your car if you go from Mumbai to Delhi and return back from Delhi to Mumbai in 10 days.
Good article..