QUESTION:
A particle of charge q is placed at a corner of a cube of the edge a.
What is the flux through (a) each cube face forming that corner and (b) each of the other cube faces?

Please Click Here for the concept behind this problem.
SOLUTION:
Given:
- a charge, q is placed at the corner of a cube of side a.
Now if the charge is considered to be positive then the direction of the electric field would be away from the charge.
Part (a)
In this part, you need to find the electric flux at the cube face containing the corner where the charge is placed.
Three faces that contain the charge q are shown in the diagram. The electric field lines due to charge q at these faces are along the plane of the faces. So, for these faces, the direction of the electric field is perpendicular to the area vector.
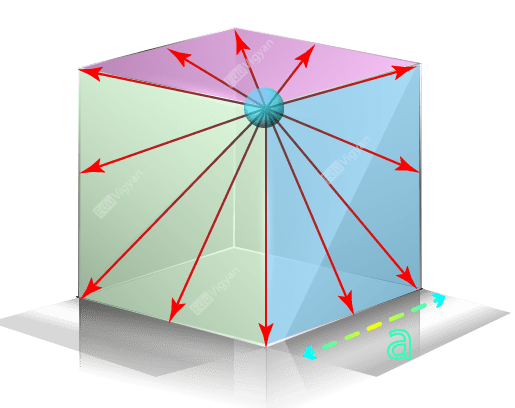
Therefore, the electric flux at each cube face forming the corner where the charge is placed is zero.
Part (b)
In this part, you need to find the electric flux at each of the other cube faces. Let’s consider an imaginary cube so that this charge will be at the center of the cube and the cube faces at which we want to find the flux will be the part of the faces of this imaginary cube.
Imagine 7 more cubes of the side length ”a” such that the charge is at the common corner of the cubes. So, the imaginary cube will be a cube of side length ”2a” containing these eight cubes as shown in the figure.

Since, the charge enclosed through the cube of side length ”2a” is;
q_{en}= q
Therefore, from the Gauss law, the total electric flux through the cube of side length ”2a” is given by;
\begin{aligned}\phi &= \dfrac {q_{en}}{\epsilon_0}\\&=\dfrac {q}{\epsilon_0}\\\end{aligned}
Since there are six faces in a cube. So, the electric flux through one face of the cube of side length ”2a” is given by;
\begin{aligned}\phi_1 &= \dfrac {\phi}{6}\\&=\dfrac {q}{6\epsilon_0}\\\end{aligned}
Now from the diagram, you can see that each face of the cube of side length ”2a” contains four faces of the cube of side length ”a” which are other than the faces containing that charged corner.
Therefore, the total electric flux through one face of the cube of side length ”a” other than the faces contains the charged corner is given by;
\begin{aligned}\phi_2 &= \dfrac {\phi_1}{4}\\&=\dfrac {\phi}{24}\\&=\dfrac{q}{24\epsilon_0}\\\end{aligned}
And this is the answer to part (b).