QUESTION:
A point charge q of magnitude 4.0\rm\ \mu C is placed at the center of the flat surface of a hemisphere of radius 10 \rm \ cm. What is the electric flux a) through the curved surface of the hemisphere and b) through the flat surface of the hemisphere?

Please Click Here for the concept behind this problem.
SOLUTION:
Given:
- q = 4.0\rm\ \mu C = 4 \times 10^{-6} \rm\ C, and
- R = 10\rm\ cm= 0.1\rm\ m.
Consider the radius of the hemisphere is R and the charge q is placed at the center of the hemisphere. So the electric field lines due to the presence of this charge are away from the charge.
Part (a)
Here you have to find the electric flux through the curved surface of the hemisphere.
Let’s imagine a Gaussian sphere of radius R (shown in the diagram) such that the charge, q is at the center of the Gaussian sphere.
This hemisphere occupies exactly half of the volume of the Gaussian sphere, and hence the curved surface area of the hemisphere will be half of the area of the Gaussian sphere.

From the above diagram, the charge enclosed through the Gaussian sphere is;
q_{en}= q
Now, from the Gauss law, the total electric flux through the Gaussian sphere is;
\begin{aligned}\phi &= \dfrac {q_{en}}{\epsilon_0}\\&=\dfrac {q}{\epsilon_0}\\\end{aligned}
Since the curved surface area of the hemisphere is half of the curved surface area of the Gaussian sphere. So, the electric flux through the curved surface of the hemisphere is;
\begin{aligned}\phi_1 &=\dfrac{\phi}{2}\\&=\dfrac {q}{2\epsilon_0}\\&=\dfrac {4 \rm\ \mu }{2 \times (8.854 \times 10^{-12} \rm\ C^2/Nm^2)}\\&=2.3 \times 10^6 \rm\ Nm^2/C \\\end{aligned}
Therefore, the answer to part (a) is;
\phi_1 =2.3 \times 10^6 \rm\ Nm^2/C
Part (b)
In Part (b), you have to find the electric flux at the flat surface of the hemisphere.
Let’s draw the electric field lines which are passing through the plane containing the flat surface of the hemisphere as you can see in this diagram.
In this diagram, the electric field is along the radially outward direction which is perpendicular to the direction of the area of the flat surface.
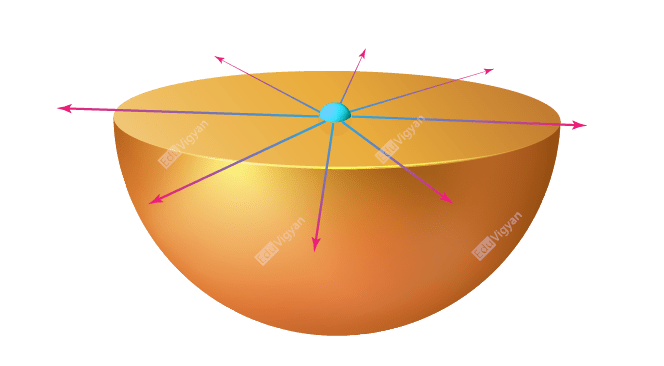
Therefore, the answer to part (b) is;
\phi_2 = 0