QUESTION:
A 10\ \rm nc charge is uniformly distributed on a ring of radius 10\ \rm cm. A sphere of radius 10\ \rm cm is constructed with its center on the circumference of the ring as shown in the figure. Find the electric flux through the sphere.

Please Click Here for the concept behind this problem.
SOLUTION:
Given:
- The charge on the ring is Q = 10 \ \rm nc = 10 \times 10^{-9}\ \rm C
- the radius of the ring as well as the sphere is R = 10 \ \rm cm = 0.1 \ \rm m
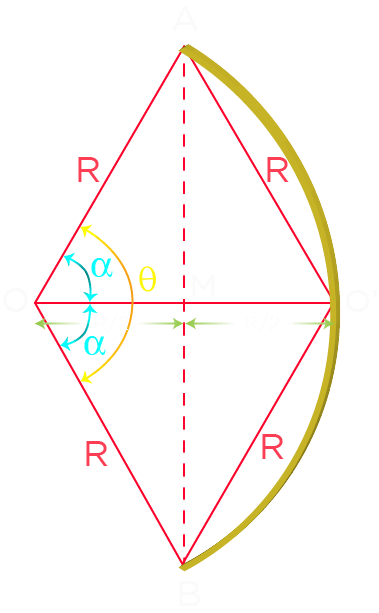
Since the ring and the sphere both have the same radius so the circumference of the sphere will pass through the center of the ring as shown in the diagram.
AO’B is the part of the ring that is inside the sphere.

In the diagram, OA, OO’ and OB are the radii of the ring and O’A, O’O and O’B are the radii of the sphere.
Since, OA = O’A so, M will be the midpoint of OO’ and hence OM = O’M = R/2.
Let \angleAOM = \angleBOM = \alpha and \angleAOB = \theta.
Here we have
\theta = 2\alpha
Now from the diagram, we can write,
\begin{aligned}R\cos\alpha &=R/2\\\Rightarrow\cos\alpha &=\dfrac {R/2}{R}\\&=\dfrac {1}{2}\\\Rightarrow \alpha &=60^o\\\Rightarrow \theta &=2\alpha\\&=120^o\\\end{aligned}
This implies that one third part of the ring is inside the sphere. So, the charge enclosed through the sphere is;
q_{en}=Q/3
Therefore, from the Gauss law, the total electric flux through the sphere is;
\begin{aligned}\phi &=\dfrac {q_{en}}{\epsilon_0}\\&=\dfrac {Q/3}{\epsilon_0}\\&=\dfrac {Q}{3\epsilon_0}\\&=\dfrac { 10 \times 10^{-9}\ \rm C}{3\times (8.854 \times 10^{-12} \ \rm C^2/Nm^2)}\\ &=3.8 \times 10^2 \ \rm Nm^2/C\end{aligned}






