Activity
Suppose you have a gun in your hand and you are going to shoot at a big wooden block (as shown in the animation below).
You notice that either the bullet comes out of the block or it fully stopped inside it. It means that the speed of the bullet is continuously decreasing while it is moving inside the block. So, there must be some reaction forces acting on this bullet that oppose its movement. If you know about the reaction forces then you can easily describe its motion by using Newton’s Law of Motion. But, in this case, suppose you really don’t have any idea about the forces and even then you want to describe the motion of this bullet then what will you do? There is a topic of Physics that describes the motion of a system without knowing about the forces that cause it to move. This famous topic is called Kinematics. So, let’s know about the equations of kinematics for a linear motion and try to describe the motion of the bullet fired by you.
First Equation of Kinematics
Since acceleration is the rate of change of velocity with respect to time, so it is given by;
\begin{aligned}a &= \dfrac{dv}{dt}\\\end{aligned}
If the particle is moving in a straight line with a constant acceleration then we can write the above equation as;
\begin{aligned}a &= \dfrac{\Delta v}{ \Delta t}\\\end{aligned}
here, \Delta v is the change in velocity in time \Delta t.
Now, if v_0 is the initial velocity, v is the final velocity and t is the time interval then this equation is converted into
\begin{aligned}a &= \dfrac{v-v_0}{t}\\\end{aligned}
After cross multiplication, it will be;
\begin{aligned}at &= v-v_0 \\\end{aligned}
which can be further written as
\begin{aligned}v-v_0 &= at \\\end{aligned}
Now, if you add v_0 on the both sides of the equation then you will get;
\fcolorbox{black}{aqua}{$v = v_0 + at$}
\textcolor{red}{(1)}
This is the first equation of Kinematics for a linear motion.
Second Equation of Kinematics
If \bar{v} is the average velocity of the particle in time interval t, then the displacement \Delta S is given by;
\begin{aligned}\Delta S = \bar{v} \times t\\\end{aligned}
Since the initial velocity of the particle is v_0 and the final velocity is v so the average velocity will be \frac{v+v_0}{2} and hence the above equation becomes
\fcolorbox{black}{aqua}{$\Delta S =\dfrac{v+v_0}{2} \times t$}
\textcolor{red}{(2)}
This is the second equation of kinematics for a linear motion.
Third Equation of Kinematics
Now, if we plug the value of v from equation 1 into equation 2, then we can write;
\begin{aligned}\Delta S &= \dfrac{(v_0 +at)+v_0}{2} \times t \\\end{aligned}
The right hand side of the above equation becomes \dfrac{2v_0 +at}{2} \times t which can be simplified as v_0t+\frac{1}{2}at^2.
The equation becomes
\fcolorbox{black}{aqua}{$\Delta S = v_0t+\dfrac{1}{2}at^2$}
\textcolor{red}{(3)}
This is the third equation of Kinematic for a linear motion.
Fourth Equation of Kinematics
Now, from equation 2, we have
\begin{aligned}\Delta S &= \dfrac{v + v_0}{2} \times t\\\end{aligned}
If we plug the value of t from equation 1 into the above equation then the equation becomes
\begin{aligned}\Delta S &= \dfrac{v + v_0}{2} \times \dfrac{v – v_0}{a}\\&= \dfrac{v^2 + v_0^2}{2a}\\\Rightarrow 2a \Delta S &= v^2 – v_0^2\\\Rightarrow v^2 – v_0^2 &= 2a \Delta S\\\end{aligned}
Now, if you add v_0^2 on both sides of the above equation then you will get;
\fcolorbox{black}{aqua}{$v^2 = v_0^2 + 2a \Delta S$}
\textcolor{red}{(4)}
The above equation is the fourth equation of kinematics.
So, these are the equations of Kinematics for a linear motion. Here it should be noticed that these equations are valid only when the motion of the particle is considered along a particular direction and the most important thing is the acceleration of the particle along that direction should be constant.
The derivation of Equations of Kinematics using Graphical Method
The equations of Kinematics can also be derived using a velocity-time graph. A velocity-time graph is shown below.
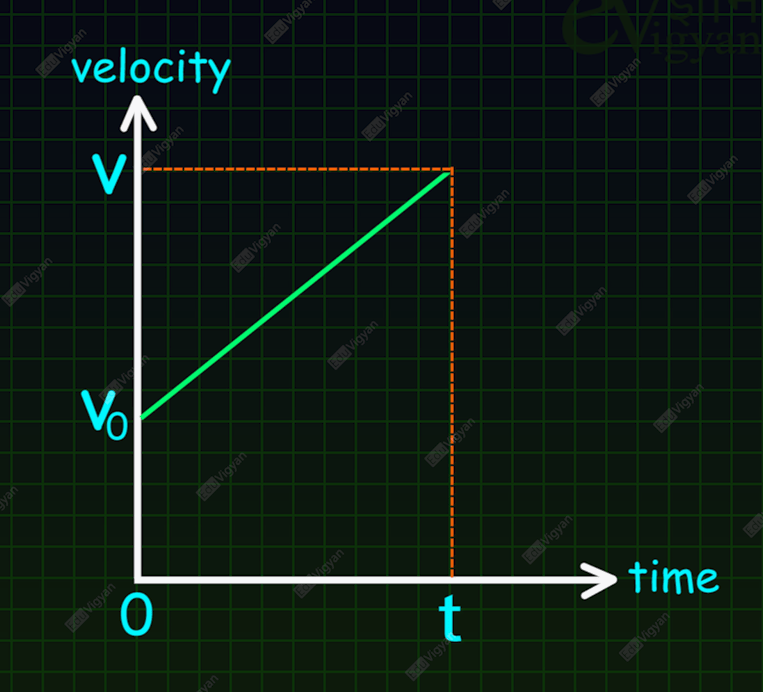

In this graph, v_0 is the velocity of an object at time t=0 and v is its velocity at time t. Since, in this diagram, the velocity-time graph is a straight line, the acceleration is constant throughout the motion
The acceleration is given by;
\begin{aligned}a &= \tan\theta\\\Rightarrow a &= \dfrac{\text{perpendicular}}{\text{base}}\\\end{aligned}
Here, the length of the perpendicular is v – v_0 and the length of the base is t so,
\begin{aligned}a &= \dfrac{v – v_0}{t}\\\Rightarrow at &= v-v_0\\\Rightarrow v &= v_0 + at\\\end{aligned}
So this is the derivation of the first equation of Kinematics by using a graphical method.
Since the displacement is equal to the area under the velocity-time graph. So, for the displacement, we need to find the area under the straight line. We can divide this area into two parts, one is a rectangle and another one is a triangle as shown in the figure below. So, the displacement, \Delta S is equal to the area of the rectangle plus the area of the triangle.
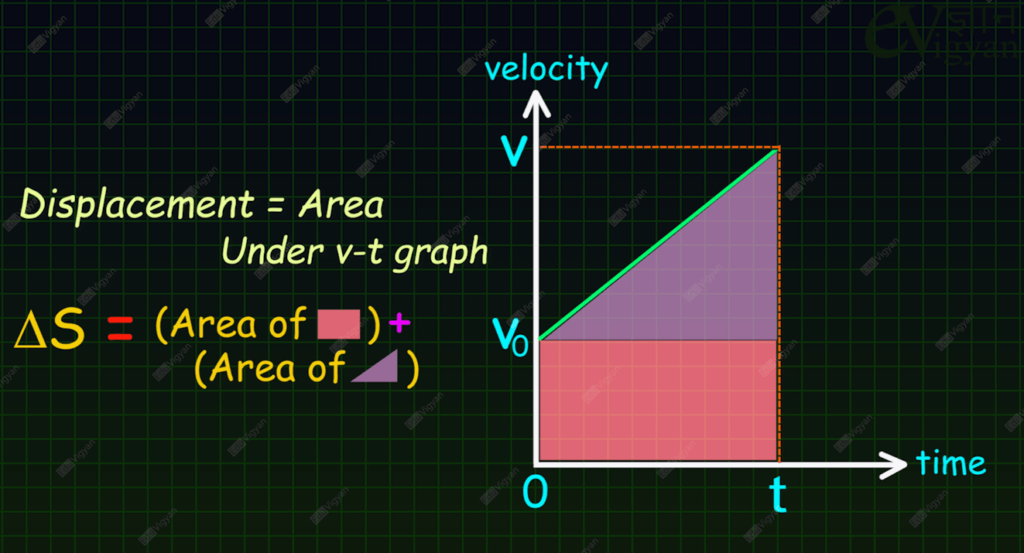
From the diagram, the area of the base is equal to \frac{1}{2} \times t \times (v-v_0).
And the area of this rectangle is equal to t\times v_0.
So, the displacement, \Delta S is given by
\begin{aligned}\Delta S &= t\times v_0 + \dfrac{1}{2} \times t \times (v-v_0)\\\end{aligned}
Since v – v_0 = at so, we have
\begin{aligned}\Delta S &= v_0t + \dfrac{1}{2} \times t \times (at)\\\end{aligned}
And finally, we have,
\begin{aligned}\Delta S &= v_0t + \dfrac{1}{2} at^2\\\end{aligned}
By using the above two equations we can also derive the remaining two equations of kinematics.
Now let’s come back to the activity.
Activity
Let’s assume that the velocity of the bullet before hitting the wooden block is 200\rm \ m/s and the bullet travelled a distance 1\rm \ m before stopping into the block. Also, assume that the rightward is a positive direction.
We have
- the initial velocity, v_o = + 200\rm \ m/s
- the final velocity, v = 0 and
- the displacement of the bullet \Delta S = + 1\rm \ m
Now let’s find the time taken by the bullet during its motion inside the block and the acceleration of this bullet.
We have four equations of kinematics that are available to us to find the acceleration and the time. They are;
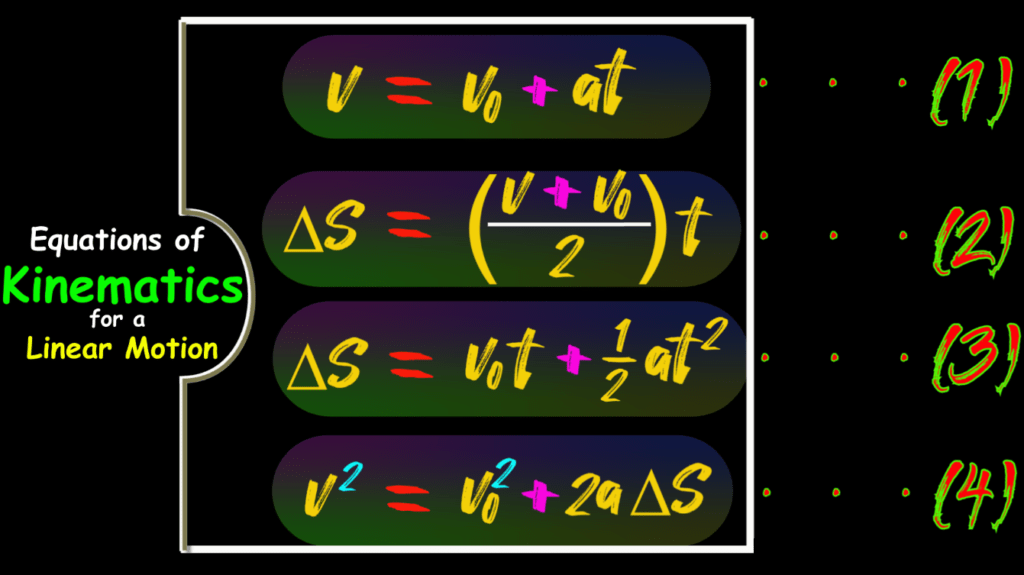
You see that there are five variables in these equations. They are v, v_0, a, t and \Delta S. And there are four variables in each individual equation.
In this problem, three variables are given, they are v, v_0, and \Delta S and we have to find the rest of two variables, a and t. So, which equation one should pick to find the unknown variables.
If you try to use the fourth equation then you can easily get the value of a because in this equation only one variable is unknown for us and that variable is a. So, from this equation, if you plug the known values then this equation becomes;
\begin{aligned}0^2 &= (200\rm \ m/s)^2 +2a \times (1\rm \ m)\\\Rightarrow -40000\rm \ m^2/s^2 &= 2a \times (1\rm \ m)\\\Rightarrow a &= \dfrac{-40000\rm \ m^/s^2}{2 \times (1\rm \ m)}\\\Rightarrow a &= -20000\rm \ m/s^2\\\end{aligned}
Here, we got the negative acceleration. It means that the direction of the acceleration is along leftward.
Now we have four variables that are known to us so, you can pick any one of the first three equations to find the unknown variable, t. Let’s pick the first equation. From this equation, if you plug the known values then this equation becomes;
\begin{aligned}0 &= 200\rm \ m/s +(-20000\rm \ m/s^2) \times t \\\Rightarrow t &=\dfrac{-200\rm \ m /s}{-20000\rm \ m/s^2} \\ &= 0.01\rm \ s\\\end{aligned}
