QUESTION:
Calculate the ratio of the electrostatic to gravitational interaction forces between two electrons, between two protons. At what value of the specific charge q/m of a particle would these forces become equal (in their absolute values) in the case of interaction of identical particle.
To solve this problem, you must have an idea of Coulomb’s Law of Electrostatic Force and Newton’s Law of Gravitation.
SOLUTION:
Here, we have two electrons and two protons and they are placed in a vacuum medium. Let’s consider q_e and m_e are the charge and mass of an electron and q_p and m_p are the charge and mass of a proton. Let r_e is the distance between two electrons and r_p is the distance between two protons.
We have:
q_e =-1.602 \times10^{-19}\ \rm C
q_p =+1.602 \times10^{-19}\ \rm C
m_e =9.11 \times10^{-31}\ \rm kg
m_p =1.67 \times10^{-27}\ \rm kg
But we don’t know r_eand r_p here.
For the case of electrons
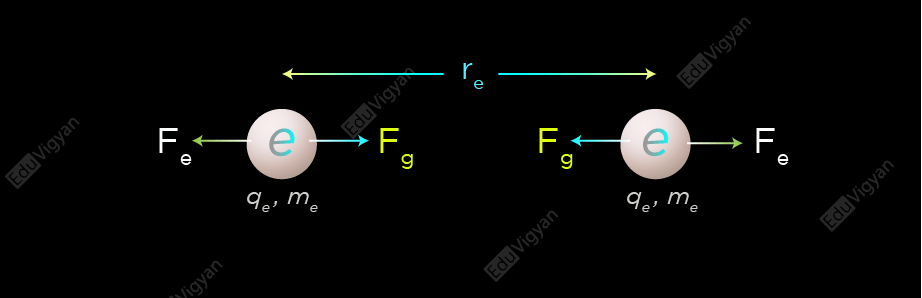
The electrostatic force between two electrons is;
F_e = \dfrac{kq_e^2}{r_e^2}
And the gravitational force between two electrons is;
F_g = \dfrac{Gm_e^2}{r_e^2}
So, the ratio of the electrostatic to the gravitational force between two electrons is given by;
\begin{aligned}\dfrac{F_e}{F_g} &= \dfrac{kq_e^2/r_e^2}{Gm_e^2/r_e^2}\\&= \dfrac{kq_e^2}{Gm_e^2}\\&= \dfrac{(9 \times10^9\ \rm Nm^2/C^2)(- 1.602 \times10^{-19}\ \rm C)^2}{(6.67 \times10^{ -11}\ \rm Nm^2/kg^2)(9.11 \times10^{-31}\ \rm kg)^2}\\&\approx4.17 \times10^{42}\end{aligned}
For the case of protons

The electrostatic force between two protons is;
F_e = \dfrac{kq_p^2}{r_p^2}
And the gravitational force between two protons is;
F_g = \dfrac{Gm_p^2}{r_p^2}
So, the ratio of the electrostatic to the gravitational force between two protons is given by;
\begin{aligned}\dfrac{F_e}{F_g} &= \dfrac{kq_p^2}{Gm_p^2}\\&= \dfrac{(9 \times10^9\ \rm Nm^2/C^2)(+1.602 \times10^{-19}\ \rm C)^2}{(6.67 \times10^{ -11}\ \rm Nm^2/kg^2)(1.67 \times10^{-27}\ \rm kg)^2}\\&\approx1.24 \times10^{36}\end{aligned}
Now let’s find the value of the specific charge q/m of any charged particle when the absolute value of electrostatic and gravitational forces between two identical charged particles become equal.
If q is the charge, m is the mass, and r is the separation between two identical charged particles then the electrostatic force between these two identical charged particles is;
F_e = \dfrac{kq^2}{r^2}
And the gravitational force between these two identical charged particles is;
F_g = \dfrac{Gm^2}{r^2}
Now, if F_e = F_g then we have;
\begin{aligned}\dfrac{kq^2}{r^2} &= \dfrac{Gm^2}{r^2}\\\Rightarrow\dfrac{q}{m}&= \sqrt{\dfrac{G}{k}}\\&= \sqrt{\dfrac{6.67 \times10^{ -11}\ \rm Nm^2/kg^2}{9 \times10^9\ \rm Nm^2/C^2}}\\&\approx0.86 \times10^{-10}\ \rm C/kg \\\end{aligned}
Therefore, the required value of the specific charge q/m when the absolute value of electrostatic and gravitational forces between two identical charged particles become equal is;
q/m =0.86 \times10^{-10}\ \rm C/kg




