Instantaneous Speed
It is the speed of a particle at any instant of time, t.
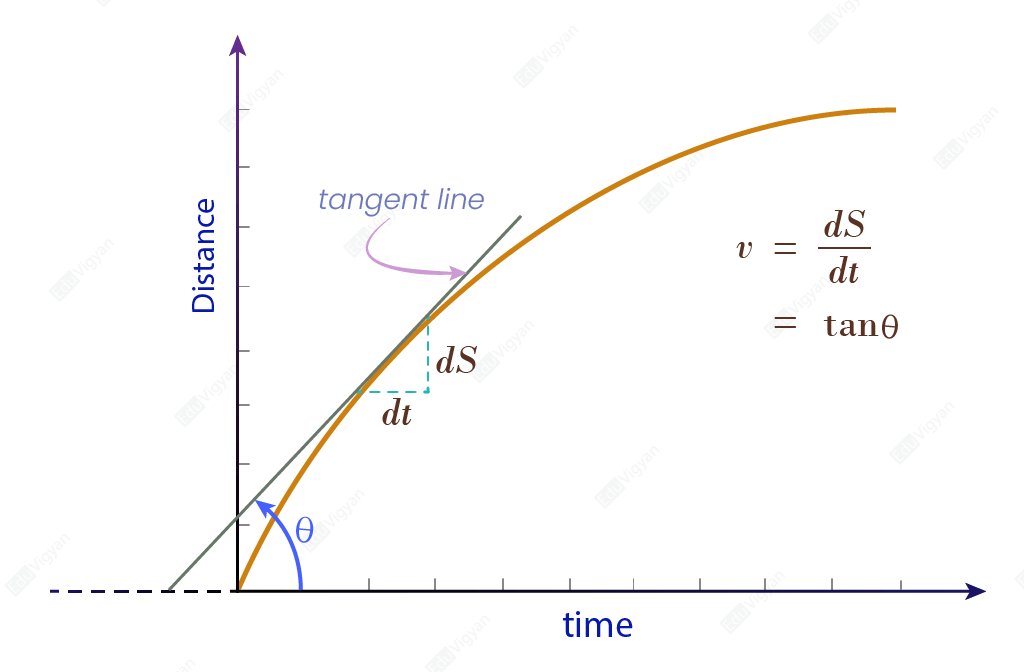
If dS is the distance traveled by the particle in a very small time, dt, then the instantaneous speed of the particle at that time is given by;
\begin{aligned}v &= \dfrac{dS}{dt}\\\end{aligned}
That is, it is the rate of change of the distance with respect to time, and hence from the differential calculus, we can say that the instantaneous speed at any time, t is equal to the slope of the tangent line on the curve in the distance-time graph at that time.
In a distance-time graph, at any time, t, if the tangent line on the curve makes an angle \theta with the time axis then the instantaneous speed at that time will be;
\begin{aligned}v &= \tan{\theta}\\\end{aligned}
Activity
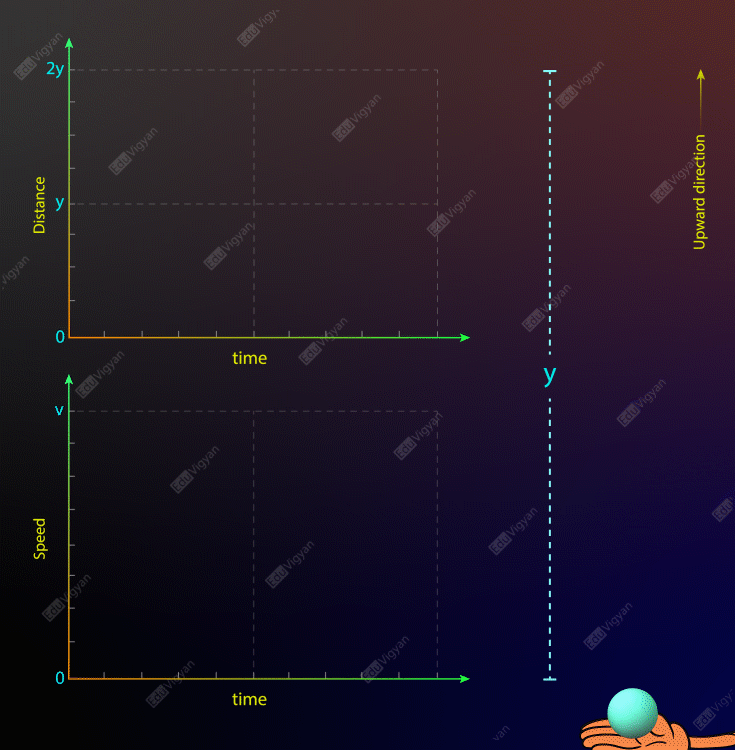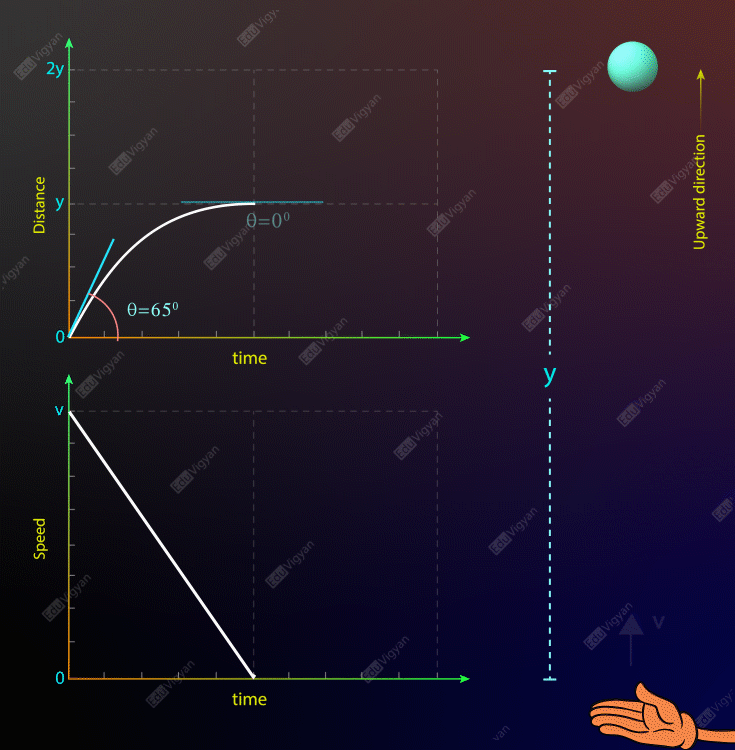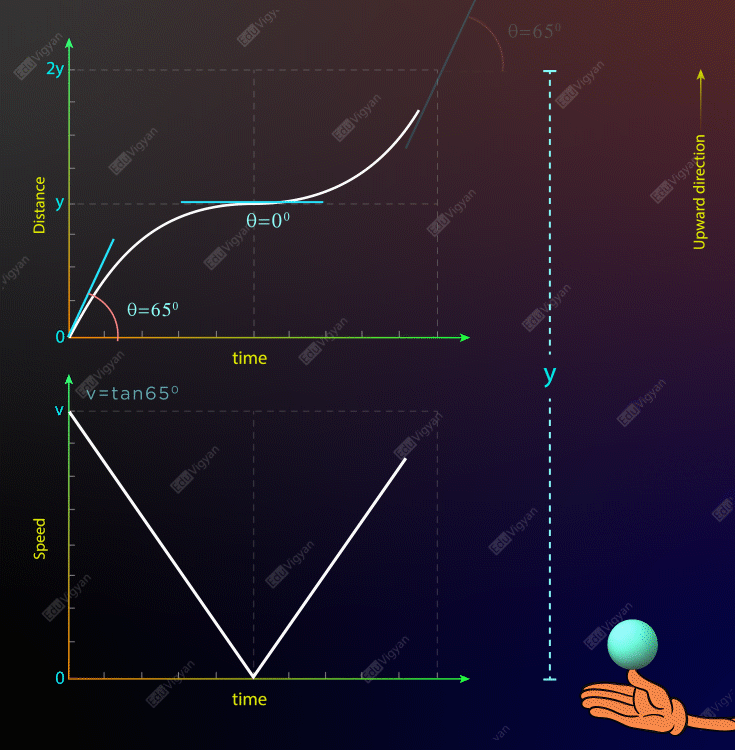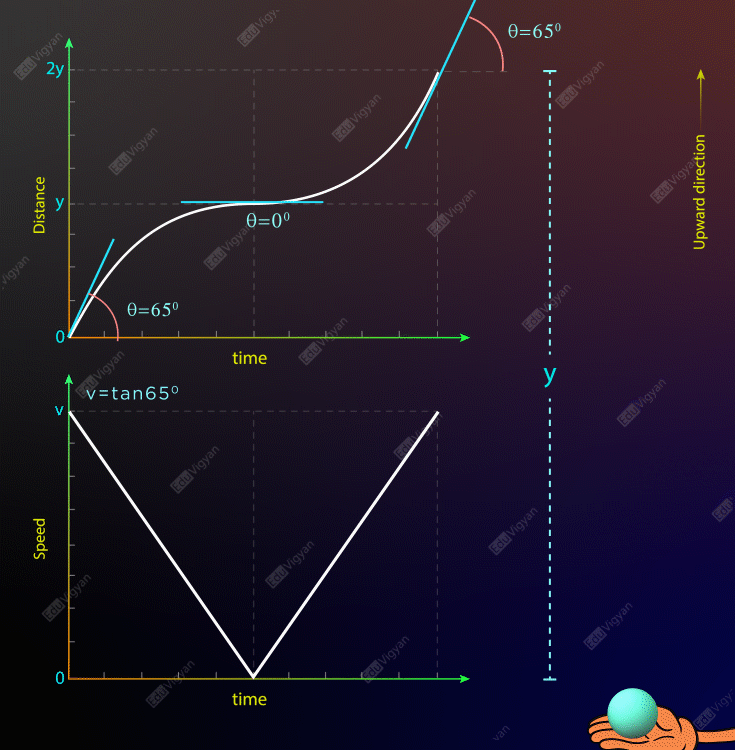
If you throw a ball along the vertically upward direction then you see that the ball first goes up and then after some time returns back into your hand. If the medium is a vacuum then the distance-time graph of the motion of the ball will look like as shown in the animation below. From this graph, it can be easily noticed that the distance traveled by the ball in a fixed time interval is more when it is at the lower position. Also, you can see that the slope of the tangent line decreases to zero while the ball is going up and increases while it is going down. So, the instantaneous speed of the ball is maximum when it is at the lowest position and zero at its highest position. A speed-time graph of the motion of this ball can be visualized in the diagram below.
Instantaneous velocity
Since speed is a scalar quantity so, it doesn’t depend on the direction of the motion of the particle and that’s why it is always positive. But this is not exactly in the case of the instantaneous velocity. Since velocity is a vector quantity, therefore, you have to take care of the direction also.
The instantaneous velocity at any time, t is given by;
\begin{aligned}\vec{v} &= \dfrac{\vec{dS}}{dt}\\\end{aligned}
Here, \vec{dS} is the displacement of the particle in a small time interval, dt.
In a displacement-time graph, the instantaneous velocity at any time, t is equal to the slope of the tangent line on the curve at that time. That is
\begin{aligned}v &= \tan{\theta}\\\end{aligned}
Activity
In the activity, we found the magnitude of the velocity (speed) of the ball is maximum when it is at its lowest position and zero when it is at its highest position. But the direction of motion of the ball is along the upward direction when it is going up and it is along the downward direction when it is going down. So, the slope of the tangent lines on the curve in the displacement-time graph will be positive during the ball is going up, will be zero at its maximum height, and will be negative during the ball is going down. The displacement-time graph and the velocity-time graph of the ball can be seen in the animation below.

Instantaneous Acceleration
In the above example, the velocity of the ball is continuously changing and hence the ball must have some acceleration. Because acceleration is the rate of change of velocity with respect to time.
The instantaneous acceleration of the ball at any time, t is given by the equation;
\begin{aligned}\vec{a} &= \dfrac{\vec{dv}}{dt}\\\end{aligned}
The acceleration of an object at any instant of time is known as instantaneous acceleration. At any time t the instantaneous acceleration is the rate of change of the velocity with respect to time. It is the slope of the tangent line on the curve in the velocity-time graph. If \theta is the angle made by the tangent line on the velocity-time curve with the time axis then the instantaneous acceleration will be;
\begin{aligned}a &= \tan{\theta}\\\end{aligned}
In the velocity-time graph of the same example, you can notice that the velocity of the ball is continuously decreasing with time, and also the curve is a straight line so, the instantaneous acceleration throughout the motion is constant.
Activity
In the activity, we found that the velocity of the ball is continuously decreasing with time, and also the velocity-time curve is a straight line so, the instantaneous acceleration throughout the motion will be constant. The velocity-time graph and the acceleration-time graph of the ball can be seen in the animation below.
But do you know? Why the velocity of the ball is changing? Why does it come back to you when you throw it along a vertically upward direction? It is because of the gravitational pull by the Earth. And that’s why this acceleration is called acceleration due to gravity.
\begin{aligned}a &= -g\\&= -9.8 \rm \ m/s^2\\\end{aligned}

