QUESTION:
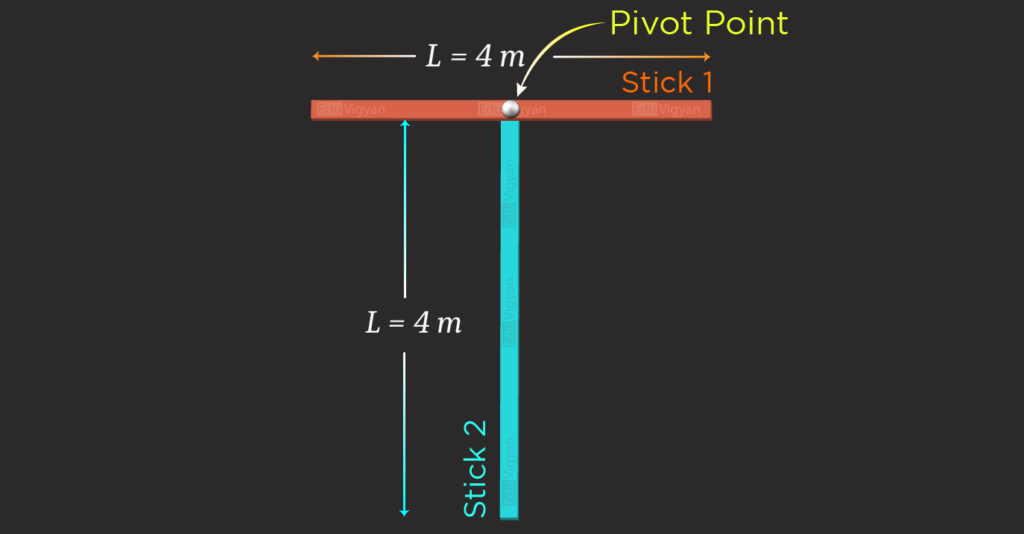
A physical pendulum consists of 4\ \rm m long sticks joined together as shown in the figure. What is the pendulum’s period of oscillation about the midpoint of the horizontal stick?

Please Click Here for the concept behind this problem.
SOLUTION:
Given:
- The length of the stick is L = 4.0\rm \ m.
Let:
- Mass of the stick is m
So, the total mass of the physical pendulum will be;
M = 2m
Now, let’s find the center of mass of the system of two sticks.
Let’s choose a coordinate system. Consider an x-y coordinate system such that the x-axis is passing through stick 1 and the y-axis is passing through stick 2 as shown in the figure.
Let C_1 be the center of mass of stick 1, C_2 is the center of mass of stick 2, and C is the center of mass of the system.
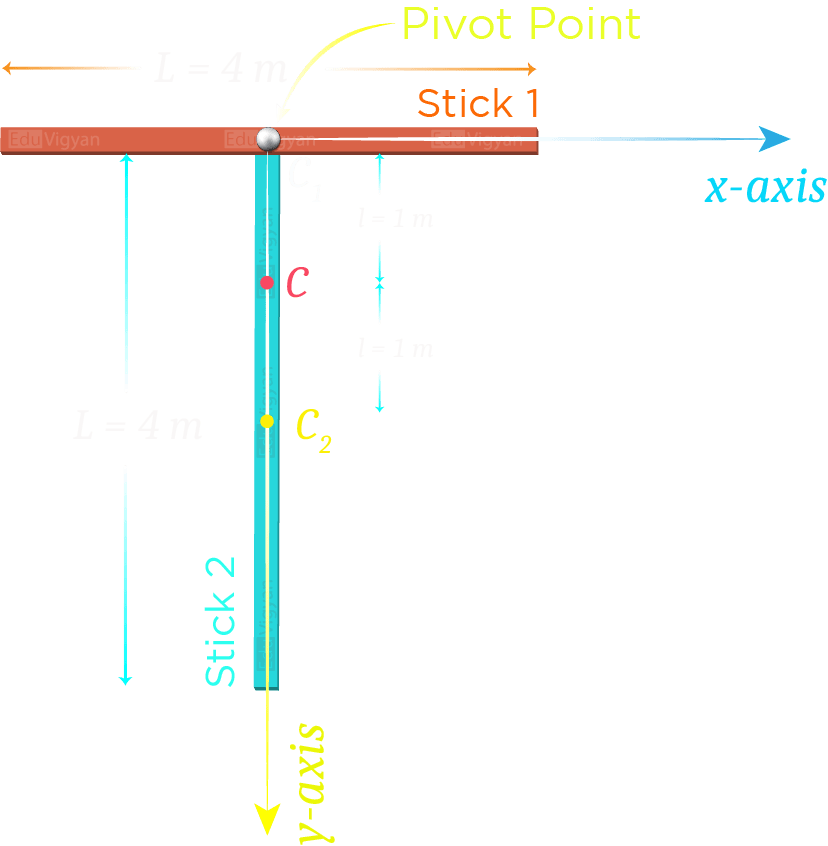
Since, C_1 and C_2 both lie on the y-axis. So, the x-coordinate of the center of mass of the system is zero Therefore, we need to find only the y-coordinate of the center of mass of the system.
The y-coordinate of the center of mass is given by;
\begin{aligned}y_{cm} &= \dfrac {\sum\limits_{i=1}^{n}m_iy_i}{M}\\&= \dfrac {m_1y_1+m_2y_2}{M}\\&=\dfrac{m\times0+m\times 2}{2m}\\&=1.0\rm \ m\\\end{aligned}
Thus the distance between pivoted point and the center of mass of the physical pendulum is;
l = 1.0\rm \ m
The moment of inertia of the stick 1 about the center of mass of the physical pendulum is given by;
\begin{aligned}\mathrm I_{1} &= \dfrac {mL^2}{12}+ml^2 \\\end{aligned}
The moment of inertia of the stick 2 about the center of mass of the physical pendulum is given by;
\mathrm I_{2} = \dfrac {mL^2}{12}+ml^2
Thus, the moment of inertia of the physical pendulum about the center of mass is given by;
\begin{aligned}\mathrm I_{cm} &=\mathrm I_{1}+\mathrm I_{2}\\&= 2 \times \left \{dfrac {mL^2}{12}+ml^2 \right \}\\&=\dfrac {mL^2}{6}+2ml^2 \\\end{aligned}
The time period of the physical pendulum is given by the expression;
\begin{aligned}T &= 2\pi \sqrt{\dfrac{I_{cm}+Ml^2}{Mgl}}\\&= 2\pi \sqrt{\dfrac{\dfrac{mL^2}{6}+2ml^2+2ml^2}{2mgl}}\\&= 2\pi \sqrt{\dfrac{\dfrac{mL^2}{6}+4ml^2 }{2mgl}}\\&= 2\pi \sqrt{\dfrac{\dfrac {L^2}{6}+4l^2 }{2gl}}\\&= 2\pi \sqrt{\dfrac{\dfrac {4^2}{6}+4\times 1^2 }{2\times 9.8\times 1}}\\&= 3.66\rm \ s\\&\approx 4\rm \ s\\\end{aligned}
This is the final answer of this question.