A physical pendulum is a kind of rigid body that can oscillate about a fixed point, just like the oscillation of a simple pendulum, but cannot be modeled as a point mass on a light string, and so its motion depends on the distribution of its mass. It is also known as the Compound Pendulum.
Consider a rigid body which has not have any defined shape as shown in the figure. It is oscillating about a fixed point. The point of oscillation is called the pivot point.
If you give a small angular displacement and leave it, it will start oscillating about the pivot point. For a vacuum medium, its motion will be the simple harmonic motion (SHM).

The free-body diagram of the physical pendulum at an angular displacement \theta is shown in the figure below.
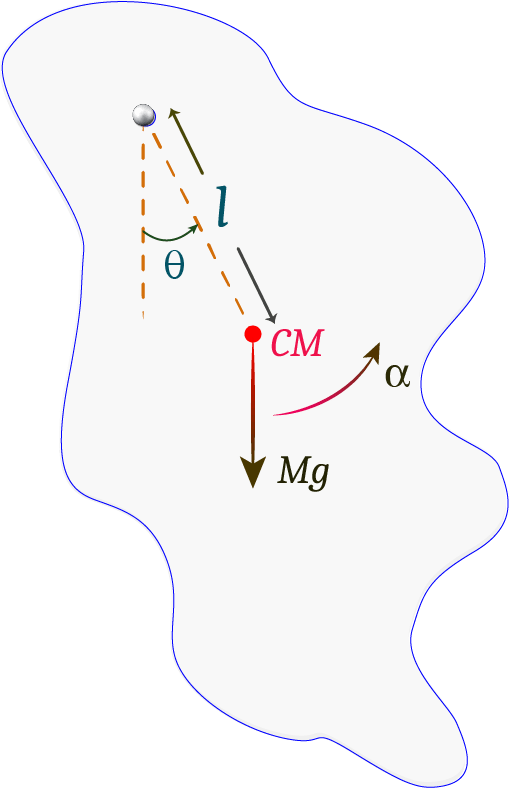
Suppose CM is the center of mass of the body and the distance of the pivot point from the center of mass is l. Let at any time, t, the angular displacement of the pendulum is \theta and the angular acceleration is \alpha.
If M is the mass of the pendulum then the gravitational force acting on the pendulum is Mg which is represented by an arrow pointing down.
If we take anticlockwise as a positive direction then the torque acting on the pendulum is;
\tau =-Mgl\sin\theta
Torque is negative because it is due to Mgsin\theta component of the gravitational force, Mg and so it is along the clockwise direction. This torque is especially known as restoring torque.
From the parallel axis theorem, the moment of inertia of this pendulum about its axis of rotation is;
I = I_{cm}+ Ml^2
Now, from Newton’s law for rotation;
\begin{aligned}\tau &= I\alpha\\\Rightarrow-Mgl\sin\theta &= I\alpha\\\Rightarrow \alpha &=-\dfrac{Mgl\sin\theta}{I_{cm}+ Ml^2}\\&\approx-(\dfrac{Mgl }{I_{cm}+ Ml^2}) \theta \\\end{aligned}
By comparing the above equation with the equation \alpha =-\omega^2 \theta (condition for the SHM), we have
\omega = \sqrt{\dfrac{Mgl }{I_{cm}+ Ml^2}}
Therefore, time period of the physical pendulum is given by;
\begin{aligned}T &=\dfrac{2\pi}{\omega}\\&= 2\pi\sqrt{\dfrac{ I_{cm}+ Ml^2}{Mg l}}\\\end{aligned}