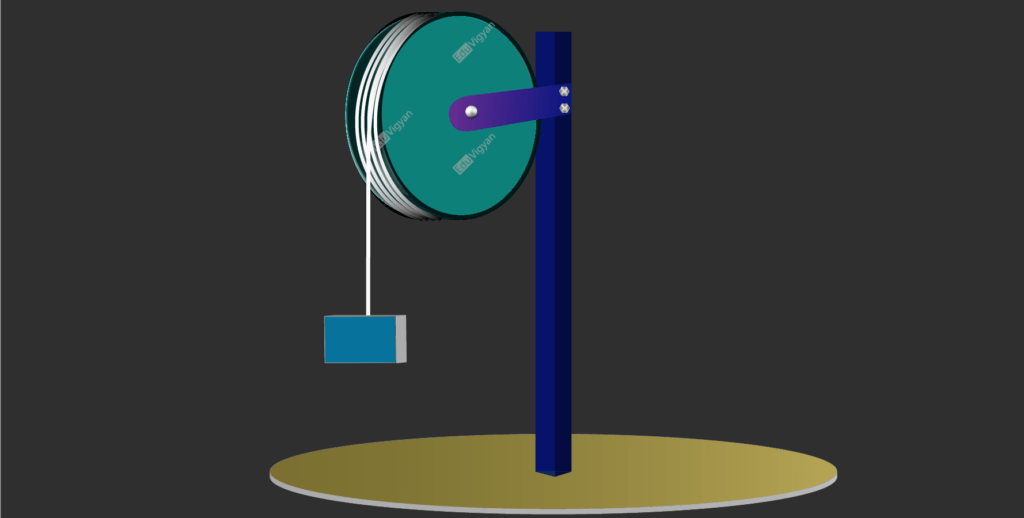
QUESTION:
A solid cylindrical pulley with a mass of M = 2\rm \ kg and radius of R = 20\rm \ cm is free to rotate about its axis. A block of mass M = 4\rm \ kg is attached to the pulley with a light string. Assume the string does not stretch or slip. Calculate (a) the tension in the string and (b) the angular acceleration of the pulley.
Please Click Here for the concept behind this problem.
SOLUTION:
Given:
- The mass of the pulley is M = 2\rm \ kg
- The radius of the pulley is R = 20\rm \ cm = 0.2\rm \ m
- The mass of the block is m = 4\rm \ kg
Let:
- a is the acceleration of the block,
- T is the tension in the string, and
- \alpha is the angular acceleration of the pulley.
Now suppose you hold the block and suddenly release it. Then it will start moving along downward and the cylinder will start rotating on its axis.
To solve this problem we need to make a free body diagram of the cylinder and the block.
For the free body diagram of the block, make the rough outline of the block, put a dot in the middle, and then draw arrows, to represent all the forces. Here, an arrow pointing down, representing the force of gravity which is mg, and an arrow pointing up, representing the tension in the string which is T.

Free-Body Diagram Of The Block
For the free body diagram of the cylinder, make the rough outline of the front view of the cylinder, put a dot at the center, and then draw arrows, to represent all the forces. Since in this case, the cylinder has only rotational motion and there is only one force that is responsible for the rotation of the cylinder which is the tension in the string that is represented by an arrow pointing down.
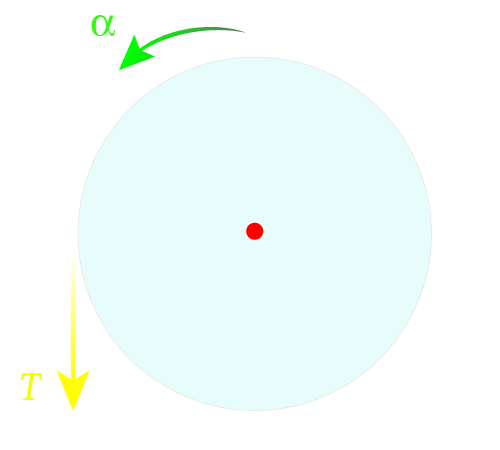
Free-Body Diagram Of The Cylinder
In the free-body diagrams, a is the linear acceleration of the block, and \alpha is the angular acceleration of the cylinder.
Applying Newton’s second law of motion for the block along the vertical direction, we have;
mg-T = ma
Applying Newton’s second law for the rotating pulley;
TR = I \alpha
Here, \ I is the moment of inertia of the pulley about its axis of rotation is given by;
I =\dfrac{1}{2} MR^2
and \ TR is the torque on the cylinder due to tension in the string.
Now, it is given in this question that the string is not slipping on the pulley. So, from no slipping condition, we have;
a = \alpha R
From equations (2), (3), and (4) we have;
a =2T/M
From equations (1) and (5) we have;
\begin{aligned}T &= \dfrac{mg}{\frac{2m}{M}+1}\\&= \dfrac{4\times 9.8}{\frac{2\times4}{2}+1}\\&= 7.84 \ N \\&\approx 8 \ N\\\end{aligned}
Therefore, the tension in the string is;
T \approx 8 \ N
And this is the answer to Part (a).
Now let’s find the angular acceleration of the pulley.
From equations (4) and (5), we have;
\begin{aligned}\alpha &= \dfrac{a}{R}\\&= \dfrac{2T/M}{R}\\&= \dfrac{2T}{MR}\\&= \dfrac{2\times 7.84}{2 \times 0.2}\\&= 39.2 \ rad/s^2\\&\approx 4 \times 10^1\rm \ rad/s^2\\\end{aligned}
Therefore, the angular acceleration of the pulley is;
\alpha\approx 4 \times 10^1\rm \ rad/s^2
And this is the answer to Part (b).
(1)
(2)
(3)
(4)
(5)