The work-energy theorem states that
the change in kinetic energy of an object is equal to the net work done by all the forces on the object.
If we divide the forces into three categories, conservative, non-conservative and external forces, then from the work-energy theorem ,
\rm W_{nc}+W_c+W_{ext.} = K.E._f \ – \ K.E._i \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{(1)}
Where
- \rm W_{nc} is the work done by the non-conservative force,
- \rm W_{c} is the work done by the conservative force,
- \rm W_{ext.} is the work done by the external force,
- \rm K.E._f is the final kinetic energy of the object, and
- \rm K.E._i is the initial kinetic energy of the object.
Further, the work done by a conservative force is the initial potential energy minus the final potential energy. That is,
\rm W_{c} = U_i \ – \ U_f \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{(2)}
Therefore, from equations (1) and (2),
\begin{aligned}\rm W_{nc} +(U_i \ – \ U_f) +W_{ext.} &= \rm K.E._f \ – \ K.E._i\\\Rightarrow \rm W_{nc} +W_{ext.} &= \rm (K.E._f \ – \ K.E._i) +( U_f \ – \ U_i)\\&= \rm (K.E._f \ + \ U_f) – (K.E_i \ + \ U_i)\\&= \rm M.E._f \ – \ M.E_i\\\end{aligned}
Here
- \rm M.E._f is the final mechanical energy of the object, and
- \rm M.E._i is the initial mechanical energy of the object.
Conservation of Mechanical Energy
From the above equation, we can say that the mechanical energy of the system is conserved if the system is only in the conservative force field. In another word, in the absence of non-conservative and external forces, the mechanical energy of the system is conserved.
Work done Under a Constant Force
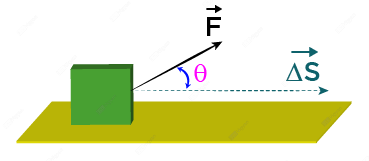
When a force moves an object over a distance then some work is done by that force.
The work done by a constant force \vec F over a displacement \overrightarrow {\Delta S} is given by the equation;
W = \vec F \cdot \overrightarrow {\Delta S} = F \Delta S \cos \theta
where \overrightarrow{\Delta S} is the displacement of the object during the application of the force and \theta is the angle between the force and the displacement.
Work done Under a Variable Force

A constant force is not obvious in the everyday world. We always observe a variable force in our daily life. Suppose F(x) is the x-component of the force acting on an object during an infinitesimal displacement dx. The work done by the force during this infinitesimal displacement is
dW = F(x)dx
The total work done by the force from the displacement x_1 to x_2 is given by
\begin{aligned}W &= \int_{x_1}^{x_2}F(x)dx\\\end{aligned}
Thus the work done by a variable force is the area under the curve on the displacement axis.
Nice i really enjoyed reading your blogs. Keep on posting. Thanks
I have read some just right stuff here. Definitely value bookmarking for revisiting. I surprise how so much attempt you set to make this sort of fantastic informative web site.
hi!,I like your writing very much! share we communicate more about your article on AOL? I require an expert on this area to solve my problem. May be that’s you! Looking forward to see you.